Brexit street art

Following on from the previous Boris Johnson and Donald Trump street art posts, keeping it political, with some of my favourite Brexit-themed graffiti and street art. Unsurprisingly, Brexit isn’t very popular with graffiti writers and street artists in London.

Typically they’re justthe likes of “Fuck Brexit”, “Bugger Brexit”, “Brexit is shit”, but there’s often some more creative examples, like the following.

//embedr.flickr.com/assets/client-code.js

This one’s a bit less obviously Brexit related, but it came just after the EU referendum in June 2016, and as Wikipedia states “Drinking the Kool-Aid” is an expression used to refer to a person who believes in a possibly doomed or dangerous idea because of perceived potential high rewards. The phrase often carries a negative connotation. It can also be used ironically or humorously to refer to accepting an idea or changing a preference due to popularity, peer pressure, or persuasion.

Boris Johnson street art

After the Donald Trump street art post I thought I’d add one for Boris Johnson (or Alexander Boris de Pfeffel Johnson as he’s known to his family).  Similar to Trump he’s easy to caricaturize, and is much despised.  I have twice as many photos of graffiti and street art featuring Johnson than I do for Theresa May, even though she was PM for 3 years and he’s only been PM for less than half that time.  And three times as many as David Cameron who was PM for 6 years!  Or maybe that’s just due to an increase in street art, and/or the amount of photos I take!

I’ve picked some of my favourites, but see all my photos of him in this Flickr album.

He’s usually depicted as a figure of ridicule, a zombie, clown, Pinocchio, Mickey Mouse etc.  But the most common graffiti is just “Fuck Boris”.  Normally just as a tag or on a paste-up, but this was the best, biggest example

And this last one, not the most exciting piece of street art to look art, but a thought provoking piece of poetry (pasted over an old plexiglassed Banksy stencil, so swiftly removed).

Donald Trump street art

Political leaders inspire some great street art, graffiti and stencils, and Donald Trump is no exception. Probably more than most other US presidents; partly because he’s so widely hated, but also so easy to caricaturise with his bright orange skin and yellow mop of hair.

I’ve photographed these whenever I see them, and collected some of my favourites here. You can see all these and more in my Flickr album. Most of these are taken around Shoreditch, London, with a few others elsewhere.

Those who do not remember the past are condemned to repeat it, Bristol







Seattle

Subdude is a prolific street artist who specialises in pillorying politicians. He’s done a lot focussing on Trump and family, so I thought I’d group the best of those separately.

Donnez-moi un break, Boris!

This catchphrase made it into the news recently after Boris Johnson used it in an interview. I think quite a few people were amused by Boris’s schoolboy-level Franglais for ‘give me a break’.

“This stuff about it being anti-democratic — I mean, donnez-moi un break,”

‘Donnez-moi un break’: Johnson says he seeks Brexit deal

This isn’t the first time he’s used this phrase though. In fact it seems to be quite a favourite of his.

Here he is using the same phrase in March 2016:
“Donnez-moi un break, as we say in Brussels”

And here’s a Boris quote out of the Daily Telegraph in November 2012, taken from The Wit and Wisdom of Boris Johnson:
“My message to M van Rumpay is donnez-moi un break, mate. The people in Brussels must have been out of their tiny minds.”

Another book of Boris quotes, The essential Boris Johnson: lend me your ears, from 2003,
“Donnez-moi un break, as we say in Brussels”

And here’s an article by Boris in the Spectator from 1994.

So it’s certainly one of his stock phrases.

Here’s some people expressing their thoughts on his most recent usage of the phrase:

Did any fellow linguists love it when Boris Johnson said “Donnez-moi un break” this past week on the news… #borisjohnson #languages #french #francophone

— Matthew Bruce (@mattbruce007) September 15, 2019

'Donnez-moi un break': it's the rehearsed spontaneity of Boris Johnson that is just so tiresome. It's one of his favourite pre-prepared bon mots (a quick thread with examples) https://t.co/tk2JSN0zmC

— William Wright (@Williamw1) September 10, 2019

I think the fact that Johnson said ‘donnez-moi un break’ on TV should be reason enough to lock him in the Tower.

— Deb (@happyspinster) September 11, 2019

Boris showing off his French: "Donnez-moi un break." https://t.co/4RvMRNC7Y2

— Dr Matthew Fraser 🇪🇺 (@frasermatthew) September 10, 2019

https://twitter.com/CatherineDVries/status/1171432293296046084

Quote of the day

‘Anybody who says this stuff about it being anti-democratic, I mean, donnez-moi un break. What a load of nonsense.’

Boris Johnson visiting a French lesson at a London primary school

— Paul Williams (@freemonotheist) September 10, 2019

https://twitter.com/EJ_Mack/status/1171843011292086272

"Donnez-moi un break" said Johnson
"Un break" exists in French. And while it can sometimes be used the same as in English, its primary meaning is "estate car" pic.twitter.com/XQ5mvpRj0H

— Duncan (@shaksper) September 11, 2019

“And anybody who says, it’s all this stuff about it being anti-democratic, I mean donnez-moi un break. What a load of nonsense.” Eton and Oxford and he talks like a second-rate car salesman……

— Jon Ryan (@vicgroves) September 10, 2019

Perhaps if you speak French this is just a common phrase, but I thought it unusual enough to do a bit more investigation. I wondered if he’d actually come up with this himself… a trawl through Google turns up this:

Firstly, here’s a song, “Break”, from 2018 by Dead Obies from Montreal, where the phrase “Donne-moi un break” is repeated several times.

And here’s another song, from 2017, “Donne-moi un break” by La Patente.

Here’s a couple blog posts from an author based in Montreal, using it in 2011 and 2015.

• Donne-moi un break!
• Hey! Donne-moi un break…

And a few other random blog posts and other sites using the phrase, or “donne-toi un break”; several (or all?) of them based in Canada

• Donne-toi un break!
• Donne-toi un break
• Mon enfant, donne-moi un break pis slaque les demandes
• Le «cowboy» Jimmy Gallant célèbre ses 45 ans de carrière
• Joseph Gordon-Levitt Says He Was Too “Snobby” To Go To Prom
• What if they called an election and nobody cared?
• Bay Area Reporter, Volume 29, Number 25, 24 June 1999

And here’s yet another song from 2006 (I think), by SemiBruce, also from Montreal, “donne moi un break”.

And way before all that, French Kiss, a Meg Ryan romantic comedy from 1995, set in Paris and Cannes.
– With this vine, I’m going to make a great vineyard and get out of this shithole.
– Donnez-moi un break. You can’t make a vineyard out of one vine.
– No, not one vine.

Google Books turns up a couple books on language. Firstly, Slang: The Authoritative Topic By Topic Dictionary Of American Lingoes From All Walks Of Life, 1998,
“Give me a break. Explained by a sixteen-year old from Connecticut: “It’s a French- class thing. Anyone with a minimal French background will recognize ‘give me a,’ and they assume that break means break. Break is French for station wagon…”

And here’s one from 1982, Language Problems & Language Planning
“Despite stigmatization, break has expanded in usage beyond the ice hockey meaning ‘break-away play’ to include ‘a pause or interruption,’ as in prendre un break and ‘a chance’, as in donnez-moi un break ‘give me a break’.”

So I think we can conclude, Boris Johnson didn’t come up with this phrase, it definitely dates back to at least 1982. And it seems fairly common in Canadian French at least (and Brussels, if we can trust Boris as a reliable source).

PHPUnit testing private properties

I just discovered something.  Normally in PHPUnit for checking any private or protected class variables, I’d use a ReflectionClass to get the property, wrapped up in a helper method like this:

public static function getProperty($object, $property)
{
	$reflectedClass = new \ReflectionClass($object);
	$reflection = $reflectedClass->getProperty($property);
	$reflection->setAccessible(true);
	return $reflection->getValue($object);
}

And then in the unit test, use that like so:

$value = ReflectionHelper::getProperty($class, 'someProperty');
$this->assertSame($expected, $value);

Instead, you can just do this:

$this->assertAttributeSame($expected, 'someProperty', $class);

Most of the methods like assertEquals, assertContains etc have an assertAttribute… version.  No ReflectionClass required.

Update: Actually since originally writing this, I learned these were deprecated in PHPUnit 8.0, and will be removed in PHPUnit 9. So if you’re using PHPUnit 7 or earlier, this technique’s still fine; but otherwise use the ReflectionClass method.

JS dates British Summer Time oddness

This must be widely documented, but I came across it today and got a bit perplexed by it. I’m sure I must have encountered this in the past, but probably a long while ago.

I was working with some date pickers and comparing the number of months between two dates and getting unexpected results. Say you do this:

date = new Date(2017, 3, 1);

You’d expect it to create a date object for the 1st April. April Fool’s! Instead it seems to create a date for the 31st March, 23:00. Here’s what I get in my browser console:

new Date(2017, 3, 1);
Date 2017-03-31T23:00:00.000Z

If I specify an additional parameter for the hours, and go for 1am, then this gives me the correct date, but with the time set to 00:00, not 01:00:

new Date(2017, 3, 1, 1)
Date 2017-04-01T00:00:00.000Z

Let’s try the same thing with the 2nd April, same problem. It seems to be subtracting 1hr from whatever DateTime I’m creating:

new Date(2017, 3, 2)
Date 2017-04-01T23:00:00.000Z

new Date(2017, 3, 2, 1)
Date 2017-04-02T00:00:00.000Z

Let’s try all the months of the year:

new Date(2017, 0, 1)
Date 2017-01-01T00:00:00.000Z

new Date(2017, 1, 1)
Date 2017-02-01T00:00:00.000Z

new Date(2017, 2, 1)
Date 2017-03-01T00:00:00.000Z

new Date(2017, 3, 1)
Date 2017-03-31T23:00:00.000Z

new Date(2017, 4, 1)
Date 2017-04-30T23:00:00.000Z

new Date(2017, 5, 1)
Date 2017-05-31T23:00:00.000Z

new Date(2017, 6, 1)
Date 2017-06-30T23:00:00.000Z

new Date(2017, 7, 1)
Date 2017-07-31T23:00:00.000Z

new Date(2017, 8, 1)
Date 2017-08-31T23:00:00.000Z

new Date(2017, 9, 1)
Date 2017-09-30T23:00:00.000Z

new Date(2017, 10, 1)
Date 2017-11-01T00:00:00.000Z

new Date(2017, 11, 1)
Date 2017-12-01T00:00:00.000Z

So we can see it’s clearly doing this for any month from April to October, inclusive. i.e. British Summer Time months. It’s not a bug as such, but just added complication to take into account when working with dates.

If we turn the date into a string, it becomes a bit clearer what’s going on, it’s converting the time into British Summer Time, i.e. GMT + 1 (your results may vary depending on your local timezone):

new Date(2017, 3, 1).toString();
"Sat Apr 01 2017 00:00:00 GMT+0100 (GMT Daylight Time)"

More specifically, the BST dates this year start 26th March and end 29th October. If we check those dates at either end of the range, we can see it’s only doing this on the dates just at the edges of that range:

new Date(2017, 2, 25)
Date 2017-03-25T00:00:00.000Z

new Date(2017, 2, 26)
Date 2017-03-26T00:00:00.000Z

new Date(2017, 2, 27)
Date 2017-03-26T23:00:00.000Z

And:

new Date(2017, 9, 28)
Date 2017-10-27T23:00:00.000Z

new Date(2017, 9, 29)
Date 2017-10-28T23:00:00.000Z

new Date(2017, 9, 30)
Date 2017-10-30T00:00:00.000Z

So in other words it’s creating me a time at BST 2017-04-01 00:00:00, but in UTC that’s 2017-03-31 23:00:00. So any Date functions we call on it like getUTCMonth could potentially give us a different value from getMonth:

new Date(2017, 3, 1).getUTCMonth()
2

new Date(2017, 3, 1).getMonth()
3

To get around this, you could just add 1 hr to any date you’re creating, either in the constructor, or with the setHours method:

date = new Date(2017, 3, 1);
date.setHours(1);

Taking care that this doesn’t mess up anything else of course.

A better approach would be, instead of just using the Date() constructor, to use it in combination with the Date.UTC() method. This gets us a value in milliseconds without reference to the local timezone.

new Date(Date.UTC(2017, 3, 1))
Date 2017-04-01T00:00:00.000Z

As the MDN documentation states:

“Note: Where Date is called as a constructor with more than one argument, the specifed arguments represent local time. If UTC is desired, use new Date(Date.UTC(…)) with the same arguments.”

Someone I work with seemed to think I’d just got confused by the fact Javascript uses zero-indexed months!

PHPUnit @usesDefaultClass

When writing unit tests for PHPUnit, you can specify a @covers annotation to indicate what function or functions a unit test is for. This can be useful to correctly identify what you’re testing, if it’s not immediately obvious from the function itself.

A while ago we used to specify the full namespace of whatever class we were testing, e.g.

class StaffServiceTest extends TestCase
{
    /** @covers \projectName\services\staff\StaffService::getStaff */
    public function testGetStaff() {...}

    /** @covers \projectName\services\staff\StaffService::addStaff */
    public function testAddStaff() {...}
}

etc.

Then realised there’s a @coversDefaultClass attribute you can specify to your test class itself. Using this means you don’t need to then repeat that path with every @covers annotation:

/** @coversDefaultClass \projectName\services\staff\StaffService */
class StaffServiceTest extends TestCase
{
    /** @covers ::getStaff */
    public function testGetStaff() {...}

    /** @covers ::addStaff */
    public function testAddStaff() {...}
}

Great stuff. I was code reviewing someone’s unit tests yesterday, and he was using the @uses annotation on all his tests, to indicate functions that were being used but didn’t need test coverage, something like:

/** @coversDefaultClass \projectName\services\staff\StaffService */
class StaffServiceTest extends TestCase
{
    /**
     * @covers ::getStaff
     * @uses \projectName\services\staff\StaffService::__construct
     */
    public function testGetStaff() {...}

    /**
     * @covers ::addStaff
     * @uses \projectName\services\staff\StaffService::__construct
     */
    public function testAddStaff() {...}
 }

Unfortunately the @uses annotation needs you to specify the full path. It struck me that it would be useful if there was an equivalent @usesDefaultClass… and it turns out there is!

Someone raised an issue to get this added to PHPUnit over 3 years ago.

So the above code could then become:

/**
 * @coversDefaultClass \projectName\services\staff\StaffService
 * @usesDefaultClass \projectName\services\staff\StaffService
 */
class StaffServiceTest extends TestCase
{
    /**
     * @covers ::getStaff
     * @uses ::__construct
     */
    public function testGetStaff() {...}

    /**
     * @covers ::addStaff
     * @uses ::__construct
     */
    public function testAddStaff() {...}
}

It’s undocumented, so I’ve raised an issue to get it added to the PHPUnit Documentation: https://github.com/sebastianbergmann/phpunit-documentation/issues/477

Animated Google Maps paths from a .csv file

I got this question on one of my previous posts, Animated paths with Google Maps, from Shivani Arora, which I thought needed its own blog post to fully answer it:

“I am working on a project in which I have to plot a moving path on the map using the coordinates. I have more than 76000 coordinates. So I tried your second example with source and destination. With that code I am getting the path, but it is taking the shorter route to reach the destination.

…

In my project I need to show a particular moving path, but not the short route.
Is there any way by which we can do that? Also, I have a .csv file for my coordinates. Can you show a code by which I can access the coordinates from a .csv file using your code?”

So, there’s two parts here.  Firstly how to deal with lots of coordinates.  And secondly how to read them from a .csv file.

For the first part, I’d say the first method from my previous post is the better solution, than using the Directions Service.  Using the Service saves you from having to store all the coordinates yourself, provided you can rely on Google’s directions matching what you need.

But if you’ve already got all the coordinates sorted, and/or you need to plot your own path rather than be able to rely on the Directions Service, then just use your own coordinates entirely.

In my example I’d hardcoded something like 300 coordinates into the javascript in the page.  More likely you should use something server-side to take care of that for you, perhaps reading them from a database.

However if you’ve got them all in a .csv file, you could just use javascript to read that for you.  Here I’m just making an AJAX request to read the file directly, and then splitting it on line endings and commas to get the data into a giant 2D array.

So firstly just load the map, then call the getCoords function.

function initialize() {
	map = new google.maps.Map(document.getElementById("map"), {
	  center: {lat: 51.4788639, lng: -0.0062897},
	  zoom: 3,
	  mapTypeId: google.maps.MapTypeId.ROADMAP
	});
	
	getCoords();
}

Secondly, the getCoords function. I’m using jQuery to make an ajax request directly to the .csv file. Just setting the dataType to text, doesn’t seem to be any problem.

function getCoords() {
	$.ajax({
		url: 'coordinates4.csv',
		dataType: 'text',
		success: function(data) {
			var lines = data.split(/[\r\n]+/);
									
			lines.forEach(function(line){
				allCoords.push(line.split(','));
			});

			var bounds = new google.maps.LatLngBounds();

			allCoords.forEach(function(coords){
				bounds.extend(new google.maps.LatLng(coords[0], coords[1]));
			});
			
			map.fitBounds(bounds);
									
			drawLine();
		}
	});
}

My CSV file contents just look like:

8.52411,76.93534000000001
8.524170000000002,76.93523
8.52424,76.93537

So I use the String.split() function to split it into an array based on line endings.
I then loop over that array, and split again, to separate out the latitude and longitude.
At this point I’m also creating a Bounds object, and extending it with each of the coordinates. This is just so the map will be fully zoomed to a level where we can see all our path at once. I’ve differed from my previous example, in that I’m not constantly updating the centre of the map here.

Once the coordinates are loaded, I call drawLine:

function drawLine() {
	route = new google.maps.Polyline({
		path: [],
		geodesic : true,
		strokeColor: '#FF0000',
		strokeOpacity: 0.7,
		strokeWeight: 2,
		editable: false,
		map:map
	});
	
	marker = new google.maps.Marker({
		map: map,
		icon: "http://maps.google.com/mapfiles/ms/micons/blue.png"
	});
	
	for (var i = 0; i < allCoords.length; i++) {
		window.setTimeout(updatePath(coords), 100 * i, allCoords[i]);
	}
}

function updatePath(coords) {
	var latLng = new google.maps.LatLng(coords[0], coords[1]);
	route.getPath().push(latLng);
	marker.setPosition(latLng);
}

So much like before; starting out with an empty Polyline. Looping over all my coordinates, making a call to the updatePath function every 100 milliseconds. Or rather, I simultaneously setup thousands of calls to the function, to take place in 100ms, 200ms, 300ms, etc.

And that’s it! I tested it initially with a few hundred coordinates. I then wrote a little script to generate 70,000 slightly random coordinates. The file’s quite large, 2.5Mb, which might take a few seconds to read via ajax. And that’s a lot of coordinates to animate on the map. I’m adding a new point to the line every 100 milliseconds, which seems pretty fast, but it means it would still take nearly 2 hours to plot all the points. It also seemed to get slightly slower and jerkier the longer it went on.

For the record, here’s the script I used to generate all those coordinates. It’s not very sophisticated, and you could get something faster in any server-side language, but I just use javascript to dump it to a textarea where I then copy it to a text editor.

function getCoords() {
	var max = 70000;
	var start = {lat: 0, lng: 0};
	
	coords = start.lat + ',' + start.lng;
	
	var lat = start.lat;
	var lng = start.lng;
	var randomLat,randomLng, newLat, newLng;
	var plusOrMinusLat = 1;
	
	var maxLat = 85;
	var minLat = -85;
		
	for (var i = 0; i < max; i++) {
		randomLat = Math.random();
		randomLng = Math.random();
		
		newLat = lat + (randomLat * plusOrMinusLat);
		newLng = lng + randomLng;
		
		if (newLat > maxLat) {
			plusOrMinusLat = -1;
			continue;
		} else if (newLat < minLat) {
			plusOrMinusLat = 1;
			continue;
		}
		
		lat = newLat;
		lng = newLng;
		coords += '\n' + lat + ',' + lng;
	}
		
	document.getElementById('coords').value = coords;
}

If the latitude exceeds 90 or -90 degrees, the map stops working. So I check we don’t exceed that limit. I actually reduced that to 85 / -85 degrees; anything beyond that goes off the map with Google Maps. I don’t need to do anything similar with the longitude; if you go beyond 360 degrees, e.g. 365 degrees, it just wraps back round to 5 degrees.

Initially I was just picking random numbers either randomly added or subtracted from the previous coordinates, but that ended up like a giant scribble. So I deliberately just keep adding until I reach the upper limit, then just keep subtracting until I reach the lower limit. The end result is a slightly squiggly pattern like this:

I’d be curious to see how Shivani’s map ends up!

Update – Here’s the map I ended up with using Shivani’s coordinates:

Crossword solver

Photo by Henry Bloomfield

Here’s a little something I built for myself, with the intention of helping to complete crosswords. It’s quite annoying when you’ve got 80 – 90% through one and with only a few obscure words left to complete.

This lets you:

• create a blank crossword
• fill out any letters in it you’ve already got
• look up words for any you’ve only got some of the letters for

It doesn’t as yet let you save them and re-load.

The front end uses jQuery; server-side it’s using ColdFusion, with a dictionary of 90,000+ words.

Anyway, here it is; let me know any feedback:

http://www.duncancumming.co.uk/crossword/

Google Maps – displaying lots of markers

I was inspired by this amazing site by Jill Hubley which uses publicly-available data of all the street trees in New York City, to see if the same data was available on the London DataStore.  I couldn’t find the same thing for the whole city, although I did find just two of the 33 borough councils had published this data on the nation-wide data.gov.uk site (but not the London-specific DataStore for some reason).

• Barnet – Tree Data file 2014
• Camden – Trees In Camden

However, while looking for the trees data, I did find a dataset of all the allotments in London.  Pretty exciting stuff, I think you’ll agree, and something I’m sure something everyone wants to see mapped.  And I thought it might be an interesting exercise in seeing how to handle slightly larger amounts of markers than I usually do, so…

Firstly, they provide the data in three different files.  Two of them are zipped bundles containing a bunch of files in formats that aren’t familiar to me, but I assume are standard for GIS software used across the public sector.  The third is just a plain-old CSV file, so that’s what I’ve gone for.

There are 741 allotment locations listed.  I’ve imported that into a Google Spreadsheet, and got rid of the columns I didn’t think were necessary.

So initially I just want to grab all this data, and add it to a Google map as standard markers with infoWindows attached.  Nothing new here.  I exported my slightly amended version of the spreadsheet as a new .csv file, then used this site here to convert that into JSON structure.  That did a pretty nice job of giving me an array with each allotment being an object like this:

{
    "Name": "Abbots Way",
    "Location": "Alongside railway line",
    "Borough": "Bromley",
    "Organisation": 0,
    "Facilities": 0,
    "Comments": 0,
    "Latitude": 51.393386,
    "Longitude": -0.047422
}

For the fields Organisation, Facilities and Comments this data seemed to be fairly inconsistent across the various councils, but mostly they were blank, which has ended up as zero in the JSON.

I then simply set this up as a JSON structure, and minified it using this site (reducing it from 206Kb to 103Kb).  At this point it makes sense to get the data via AJAX, rather than embed this as a giant variable into my javascript code.  I’m using jQuery’s $.ajax() method instead of their $.getJson() method, just because I’m running this locally, not using a webserver, and I needed to specify the mimetype using the beforeSend callback (thanks to this answer on StackOverflow).

$.ajax({
	dataType: "json",
	url: 'allotments-min.json',
	beforeSend: function(xhr){
		if (xhr.overrideMimeType) {
			xhr.overrideMimeType("application/json");
		}
	},
	success: function(data) {
		var allotments = data.allotments;

		for (var i = 0; i < allotments.length; i++) {
			createMarker(allotments[i]);
		}

		map.fitBounds(bounds);
	}
});

Then I simply add the markers, setup an event listener to update the infowindow with the relevant content, and extend the map’s bounds to fit them all in:

function createMarker(allotment) {
	var marker = new google.maps.Marker({
		position: {lat: allotment.Latitude, lng: allotment.Longitude},
		map: map,
		title: allotment.Name
	});

	bounds.extend(marker.getPosition());

	var content = '<strong>' + allotment.Name + '</strong><br>';
	if (allotment.Location) {
		content += 'Location: ' + allotment.Location + '<br>';
	}
	if (allotment.Borough) {
		content += 'Borough: ' + allotment.Borough + '<br>';
	}
	if (allotment.Organisation) {
		content += 'Organisation: ' + allotment.Organisation + '<br>';
	}
	if (allotment.Facilities) {
		content += 'Facilities: ' + allotment.Facilities + '<br>';
	}
	if (allotment.Comments) {
		content += 'Comments: ' + allotment.Comments + '<br>';
	}

	marker.addListener('click', function() {
		infowindow.setContent(content);
		infowindow.open(map, this);
	});
}

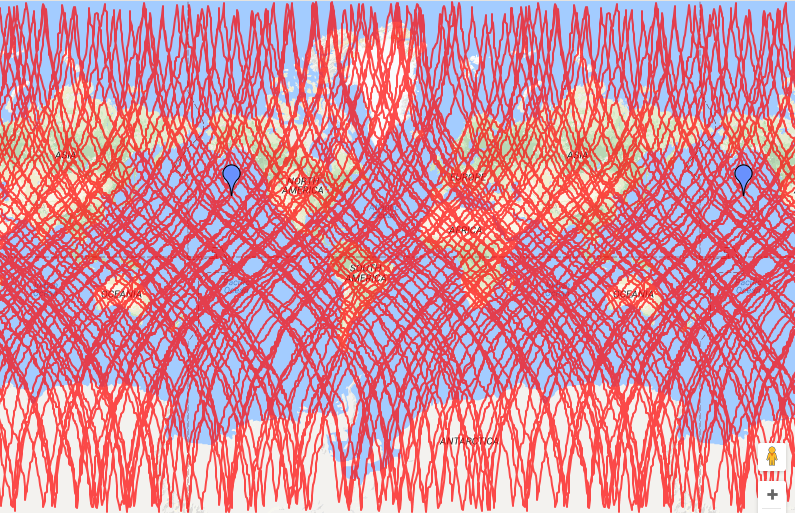
And this produces a map that looks like this:

Well that works, and it’s simple, but there’s really too many markers tightly grouped together, and you can’t filter them down by Borough for instance.  What can we do to improve this?  The Google Maps API documentation lists several things you can do when working with large datasets.  Let’s try a KML Layer.  I need to convert my data to a KML format for starters.  I used this handy site to do that for me, turning my 59Kb .csv file into a 466Kb .kml file.  Each allotment now turned into an XML structure like this:

<Placemark>
	<name>Abbots Way</name>
	<ExtendedData>
		<SchemaData schemaUrl="#csv_20160528085652">
			<SimpleData name="Name">Abbots Way</SimpleData>
			<SimpleData name="Location">Alongside railway line</SimpleData>
			<SimpleData name="Borough">Bromley</SimpleData>
			<SimpleData name="Organisation"></SimpleData>
			<SimpleData name="Facilities"></SimpleData>
			<SimpleData name="Comments"></SimpleData>
			<SimpleData name="Latitude">51.393386</SimpleData>
			<SimpleData name="Longitude">-0.047422</SimpleData>
		</SchemaData>
	</ExtendedData>
	<Point>
		<coordinates>-0.047422,51.393386</coordinates>
	</Point>
</Placemark>

Great! So according to Google’s docs, it’s simply a case of adding a KmlLayer like so:

var kmlLayer = new google.maps.KmlLayer({
	url: 'http://www.example.com/allotments.kml',
	map: map
});

Firstly the KML file has to be publicly accessible, so I had it uploaded to my server (I’m only running the HTML file locally on my laptop).  However it didn’t like that; I had to add KML (application/vnd.google-earth.kml+xml) to my list of mime types in IIS, otherwise I got a 404 error.

This still didn’t seem to work, and I stumbled across something which suggested any KML file over 10Kb should really be turned into a KMZ file instead.  That was simply a case of zipping up the KML file, and changing the file extension to .kmz.  Oh, and then adding KMZ (application/vnd.google-earth.kmz) as a mime type in IIS as well.

This still didn’t give me my full results; markers appear, but clicking each one just gave me the title, none of the other data.  Turns out the lovely KML format I was working with contained lots of elements Google Maps API aren’t supporting (here’s the full list of what they do).  So I had to reformat it, mainly replacing all the SimpleData elements with Data elements instead, and getting rid of a Schema declaration at the top, and ending up having each allotment in this format:

<Placemark>
	<name>Abbots Way</name>
	<ExtendedData>
		<Data name="Name"><value>Abbots Way</value></Data>
		<Data name="Location"><value>Alongside railway line</value></Data>
		<Data name="Borough"><value>Bromley</value></Data>
		<Data name="Latitude"><value>51.393386</value></Data>
		<Data name="Longitude"><value>-0.047422</value></Data>
	</ExtendedData>
	<Point><coordinates>-0.047422,51.393386</coordinates></Point>
</Placemark>

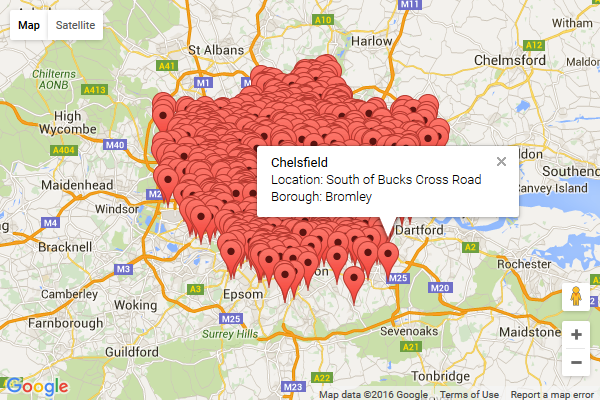
Finally that started working, giving me this kind of result…

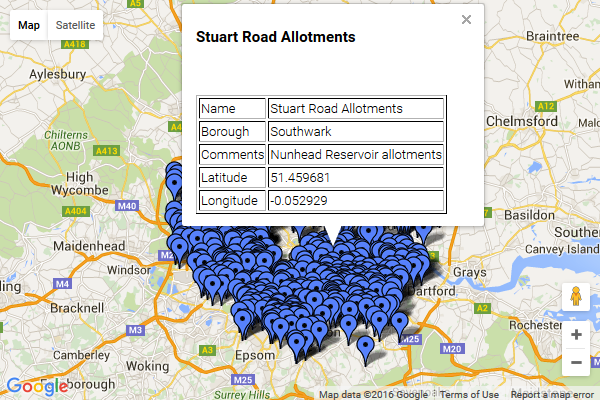
At this point there’s steps I could take to tidy up the layout of the infoWindow, but why bother?  End result: a lot of faffing around for not much different from before.  In retrospect, it seems KML is really a format more for the benefit of Google Earth than Google Maps, and I’m not sure I came up with anything useful just by changing my code to use that file format.  Other than learning what’s needed to use KML files with the Google Maps API for future reference.

What about applying some marker clustering just to reduce the huge number of markers?  That’s not too tricky, I just set everything up like in my original example, included the MarkerCluster JS file, and added this line in after I’d put all the markers into an array:

var markerCluster = new MarkerClusterer(map, markers, {imagePath: 'markerclusterer/images/m'});

The only gotcha I had was I needed to add the imagePath for the marker images to appear correctly (you may not need this, depending where your JS file is).  And this then gave me:

Zooming in a bit you start to see different icons and individual markers, e.g.

Well a bit better for reducing the amount of markers displayed at any one time, and giving you an idea of how they’re grouped across the city, but still far from ideal.  What I really want is to break it down by the various boroughs.

Next step, FusionTables.  This article by Dan Nguyen was very useful: Intro to Data Mashing and Mapping with Google Fusion Tables.  It took a bit of trial-and-error, importing data from Google Spreadsheets to Google FusionTables.  I ended up with one file in Google Spreadsheets. It contained two spreadsheets:

One with all 741  allotments and their coordinates:

The other with all 33 boroughs and the coordinates for the polygons defining their boundaries:

This data came from this publicly-available KML file; I’m not sure how accurate or up-to-date that is, and it may not tally with the data to do with the allotments (e.g. boundary changes since that KML file was made may put some allotments in the wrong councils on the map).  In this second sheet I added a new column, for a count of the allotments per borough.  This used a simple formula, using COUNTIF to tally up how often the name of each council appears in the other sheet:

=COUNTIF(Allotments!C2:C742,A2)

You’ll notice in the above screenshot that in the row for Bromley the ‘geometry’ column is blank; this was also the case for several of the other councils.  It seemed to be a problem importing from the KML file into Google Spreadsheets.  I think I ended up turning this into a FusionTable, then manually editing the values for any missing polygons.

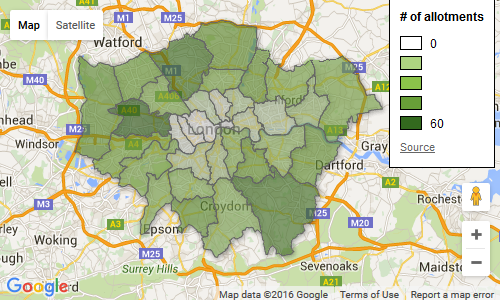
So at this point I imported both the spreadsheets into FusionTables as separate tables.  In FusionTables you get an option to turn your table into a map.  You can then choose Publish > Get HTML and JavaScript, and get all the code you’d need to turn that into a web page.  Doing that with each of these tables, I got two separate maps;

One with all the council boundaries:

And the other with small markers for all the allotments:

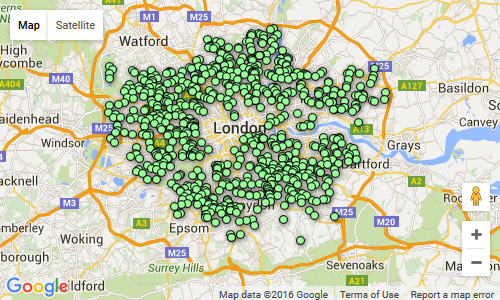
In Fusion Tables it was easy to setup the colour schemes and add the ‘# of allotments‘ legend.  All I need to do now is combine both of these into one map.

So initially I want to just display the council boundaries, so this FusionTablesLayer does that:

var boroughsLayer = new google.maps.FusionTablesLayer({
    map: map,
    suppressInfoWindows: true,
    query: {
        select: 'geometry',
        from: '15nhaHjAOYp2CrBJRJoP5bXkytmgfuRXYvGwsIuIk'
    },
    styles: [{
        where: 'count = 0',
        polygonOptions: {
            strokeColor: '#000000',
            strokeOpacity: 0.3,
            strokeWeight: 1,
            fillColor: '#edf8e9',
            fillOpacity: 0.1
        }
    },{
        where: 'count > 0',
        polygonOptions: {
            strokeColor: '#000000',
            strokeOpacity: 0.3,
            strokeWeight: 1,
            fillOpacity: 0.5,
            fillColor: '#bae4b3'
        }
    },{
        where: 'count > 15',
        polygonOptions: {
            strokeColor: '#000000',
            strokeOpacity: 0.3,
            strokeWeight: 1,
            fillOpacity: 0.5,
            fillColor: '#74c476'
        }
    },{
        where: 'count > 30',
        polygonOptions: {
            strokeColor: '#000000',
            strokeOpacity: 0.3,
            strokeWeight: 1,
            fillOpacity: 0.5,
            fillColor: '#31a354'
        }
    },{
        where: 'count > 45',
        polygonOptions: {
            strokeColor: '#000000',
            strokeOpacity: 0.3,
            strokeWeight: 1,
            fillOpacity: 0.5,
            fillColor: '#006d2c'
        }
    }]
});

The query gets all the polygon data.  Then we want to give each polygon a different style based on the number of allotments.  If you omit the ‘where’ part, you can set a default style; however you can only set up to 5 of these styles, and because I’m wanting five different colours based on the allotment count, I need to just specify all the styles for each possible option (and so I end up repeating all the properties apart from the fillColors).

This is the HTML for the map and legend:

<div id="map"></div>
    
<div id="legend">
    <p id="legend-title"># of allotments</p>
    <div>
        <span class="legend-swatch" style="background-color: #edf8e9"></span>
        <span class="legend-range">0</span>
    </div>
    <div>
        <span class="legend-swatch" style="background-color: #bae4b3"></span>
        <span class="legend-range">1 - 15</span>
    </div>
    <div>
        <span class="legend-swatch" style="background-color: #74c476"></span>
        <span class="legend-range">16 - 30</span>
    </div>
    <div>
        <span class="legend-swatch" style="background-color: #31a354"></span>
        <span class="legend-range">31 - 45</span>
    </div>
    <div>
        <span class="legend-swatch" style="background-color: #006d2c"></span>
        <span class="legend-range">46+</span>
    </div>
</div>

The values for the fillColor property obviously match up with the background colours on the legend. This adds the legend onto the map:

map.controls[google.maps.ControlPosition.RIGHT_TOP].push(document.getElementById('legend'));

Now what I want is if you click on any of the councils, it shows you just the allotments there.  This does that:

allotmentsLayer = new google.maps.FusionTablesLayer();

boroughsLayer.addListener('click', function(FusionTablesMouseEvent) {
    allotmentsLayer.setMap(null);
    
    allotmentsLayer.setOptions({
        map: map,
        query: {
            select: 'col6',
            from: '1kBhYAiZGBsIzZ-iXQZ0VC8Lhr32IUf_WOp-cYntm',
            where: "'Borough' = '" + FusionTablesMouseEvent.row.name.value + "'"
        },
        options: {
            styleId: 2,
            templateId: 2
        }
    });
});

So firstly I’ve got a global variable for the allotmentsLayer.  Each time I click a new council, I set its map property to null, removing any markers that were previously visible.  The FusionTablesLayer‘s click event handler gives you a FusionTablesMouseEvent, which lets you know which row in the FusionTable that equates to.  From this, I can get the name of the council, and I can then use that to query the FusionTable with all the allotments.

I’m also specifying an options property on the layer here.  This isn’t documented in the Maps API, but when you get the generated HTML + Javascript from FusionTables, it includes those depending on how you style your markers.  And they seemed to be required; I wasn’t able to style my markers otherwise from what I could see.

What I’m also doing is outputting the name of the council and the number of allotments it contains.  And providing a ‘show all‘ link so you can see all the allotments at any time.

<div id="borough">
    <strong id="name"></strong> <span id="count"></span>
    <p><a href="" id="showAll">Show all allotments</a></p>
</div>

I wrap these up in a div and treat it like the legend, and add it directly onto the top-middle of the map:

map.controls[google.maps.ControlPosition.TOP_CENTER].push(document.getElementById('borough'));

And in the click event listener, I update the value of the HTML:

$('#name').text(FusionTablesMouseEvent.row.name.value + ': ');
$('#count').text(FusionTablesMouseEvent.row.count.value + ' allotments');
$('#showAll,#borough').show();

The ‘show all allotments‘ link has its own event listener, which just does the query again, but without a ‘where’ clause:

$(document).ready(function() {
    $('#showAll').on('click', showAllAllotments);        
});

function showAllAllotments(event) {
    event.preventDefault();
    $('#showAll,#borough').hide();
    
    allotmentsLayer.setMap(null);
        
    allotmentsLayer.setOptions({
        map: map,
        query: {
            select: 'col6',
            from: '1kBhYAiZGBsIzZ-iXQZ0VC8Lhr32IUf_WOp-cYntm'
        },
        options: {
            styleId: 2,
            templateId: 2
        }
    });
}

And what all this gives is this:

You can see it working here.  This is more or less what I was hoping to end up with.  I would have liked to fit the bounds of the map to fit each council as it was selected.  And to have a list of all the councils, perhaps as a dropdown you could choose from.  I’m sure  these things must be possible.

From a data point of view, it would be good to include things like the length of the allotment waiting lists, or to have slightly more useful data about each allotment than just what the DataStore provided.

Next steps:

• use a different mapping system such as CartoDB or MapBox
• map what tree data is available for London

Some useful resources:

• Too Many Markers, an article by Google Maps developers mostly about marker clustering
• ColorBrewer, a colour scheme picker for maps
• Google Maps Developers Live: High-performance Geospatial Visualizations using WebGL
• Google Maps Developers Live: A Journey of 245k Points
• Google I/O 2012 – Spatial Data Visualization
• A survey of national allotment waiting list times
• Growing back to the future: allotments in the UK, open data stories and interventions